Atwood's Machine
the simplest way to measure the acceleration due to gravity is a drop test, but human error in the timing leads to inaccurate measurements. A device called Atwood's machine slows down the acceleration in a predictable way, allowing for easy measurements. The device is a pulley with 2 unequal masses attached on either side by a string. A short demo is available here.

From here, we need to draw free-body diagrams of each component, both blocks have the same acceleration because the string has a constant length. The edge of the pully must also be the same because it's in contact with the string. The coordinate system was chosen to have the direction of motion give a positive acceleration as shown in green.
If the pulley is not massless, some torque is needed to accelerate it (see eq3 below) resulting in a different tension on either side of the pulley. If it is massless, set MOI "I" equal to 0 in the final equation.
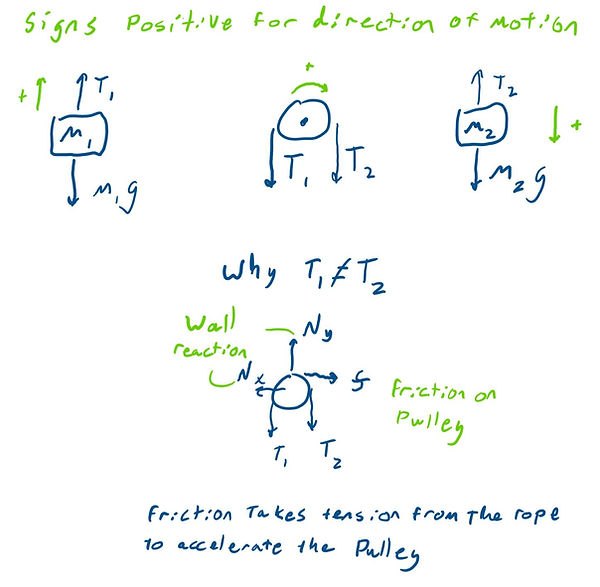
From each FBD, newtons laws are applied in the direction of motion (y-axis for eqn 1 and 2, right-hand torque for eq3) and algebraically solved for the unknown gravitational acceleration. eqn 3a uses an equation from the rotation page. In a lab, your experiment would measure the displacement of the machine and elapsed time; the equation for measured acceleration is also provided.

In real life, other variables can affect the expriment. The most important are: bearing friction on the pully, air resistance, and the mass of the string.
High bearing friction can prevent the pully from moving when released, increasing the elapsed time, making gravity appear weaker.
Air resistance slows the system at high velocity, so the faster it moves, the less accurate the equation becomes.
Having too much or too heavy string pulls toward whatever side is longer, this can result in a lower acc at the start when m1 is low, but a high acc at the end when m2 has more string.
These can be accounted for in equations 1,2, and 3 but are dependent on velocity and position, so differential equations need to be applied and there may not be an algebraic solution.