Block on a slope (static)
There are many variations of this problem, with applied forces pointing in any direction, positive or negative slope, with friction or smooth. The work in blue will show a general solution to the FBD and equations of motions to all of these. Comments are shown in green, example values in red. Solving for further unknowns is up to you.
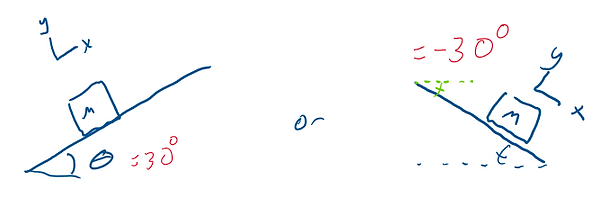
As theta is CCW positive on the unit circle, its useful to use the same sign convention for positive or negative slope. It's also useful to rotate the coordinate system by the same amount. It's possible to solve with a straight coordinates, but it usually includes a system of equations, and makes solving for acceleration (in a non static problem) a lot harder.
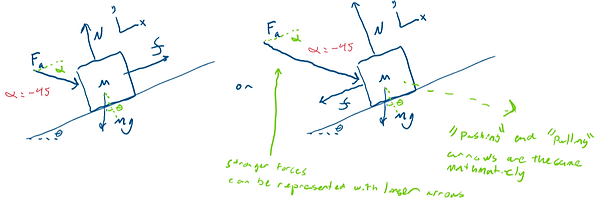
Next, your free body diagram will look something like this (theta can be negative for a down slope). The hard part here is that friction (curly f) will oppose the direction of the rest of the forces acting in the x-direction (for static friction).
The two cases shown are for when the x component of the applied force (F_a) is weaker than the x component of the weight (mg), friction "holds it up". The 2nd picture is if the applied force is stronger, friction opposes upward motion.
The applied force can point in any direction, with the most common being parallel to the slope (alpha =0) or actually horizontal (alpha = --theta). Still, it can point in any direction, including backward (over 90 degrees). For drawing's sake, I used -45 degrees with respect to x, which is 15 degrees below horizontal.
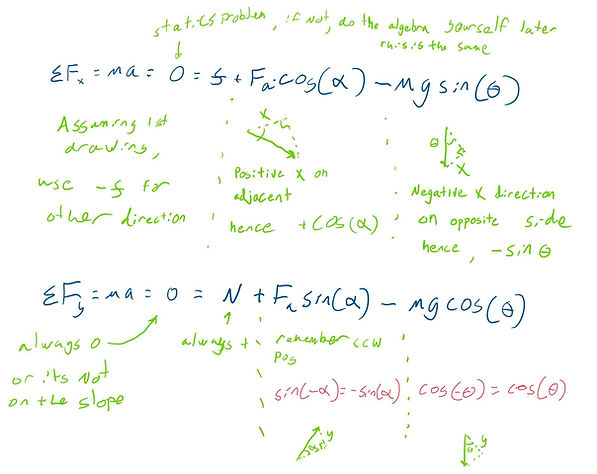
Keep in mind the sign conventions used here, if you're not sure if it's right, read the trig section of this page. (I wish I could make section links like Wikipedia)
Also, note that friction = mu* normal (f=μ*N)
From here, we can solve for whatever unknowns are missing. The most common is the relationship between μ and theta with no applied force (below), or minimum and maximum applied force (fixed angle) to keep static (below that).
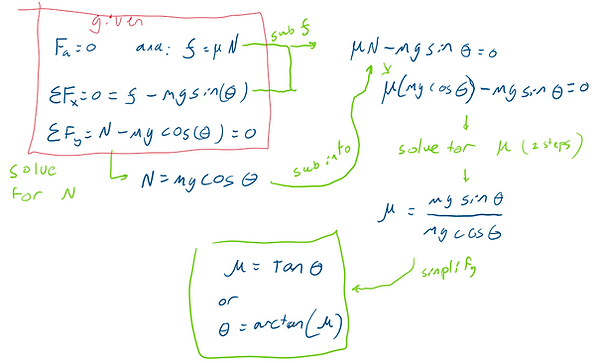
Note that slip angle does not depend on mass or gravity, with no applied forces, if there are applied forces, a system of equations is required, and mass and gravity must be known.
But if the angle is known, there will be a minimum applied force (a large negative is still a minimum) to keep it from going down the slope, and a maximum that can be held in place by friction. First, let's do the setup for the minimum applied, where the weight is the dominant force.

This equation still works if the applied force is down the slope, just use alpha = 180, or if the slope is going down (theta is negative) keep in mind the reference angles I did the setup with.
For finding the maximum force, you could go all the way back to the free body diagram and change the direction, then do this whole thing again, but there's an easier way! Looking through all the algebra we did, the sign of f carries through the whole equation (no nonlinearities, like squares and trig functions), while weight and applied force are the same. In the final equation friction force is the 2nd term in the numerator and denominator, so changing the sign of each term is equivalent to changing the direction of friction.
